Instructions to Play Iterated Prisoner’s Dilemma

Iterated Prisoner’s dilemma is a fun game to play as long as you’re with the right people as well as if you have the right setting and rules for this game. There are a lot of reasons for you to want to play iterated prisoner’s dilemma, but the hard part can definitely be finding the right players as well as understanding the rules, setting as well as how all of the parties should act.
In order for you to play this game, you’re going to have to learn the rules of this game so that you can play Iterated prisoner’s dilemma properly and have fun. So, if you’re looking for instructions for how to play Iterated prisoner’s dilemma, then you’ve definitely come to the right place. Keep reading for you to find out and enjoy playing.
- Find The Right People
I’m pretty sure that this is obvious, but a game is much more fun if you’re playing it with the right people. Find people who you enjoy spending time with, and that will surely make playing iterated prisoner’s dilemma much more enjoyable and memorable for all of the players. Finding people is easy. There are mutually mind apps such as some to find local fuck buddies through free fuck app that can certainly help you and there are other apps for other finding purposes. Normally, the minimum number of players that you can have for this game would be three, but the more, the merrier, right? Just as long as you have fun, you can definitely have more players in this game.
- Know The Setting
Knowing the setting is important as well. Know where you should hold this game, and it should be a reasonable and appropriate place—looking for a place that has two rooms that can separate two people, or at least a place where two people won’t be able to communicate with each other. If you can’t find a place available that at least has two rooms, you can definitely just separate the two in different ways by putting curtains or other similar items in order to separate them.
- Get To Know The Rules

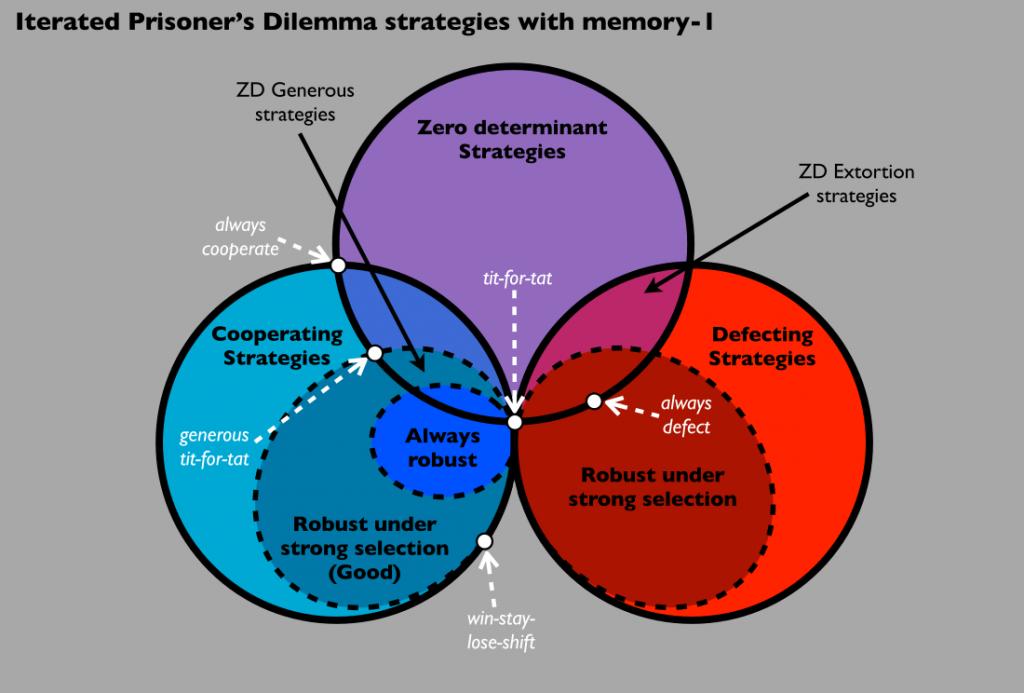
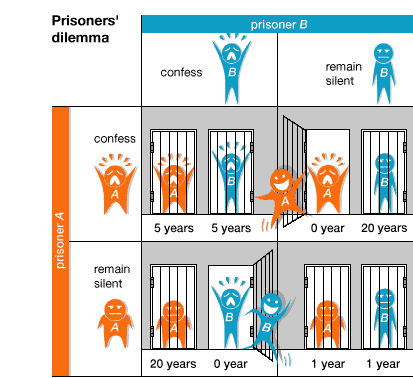
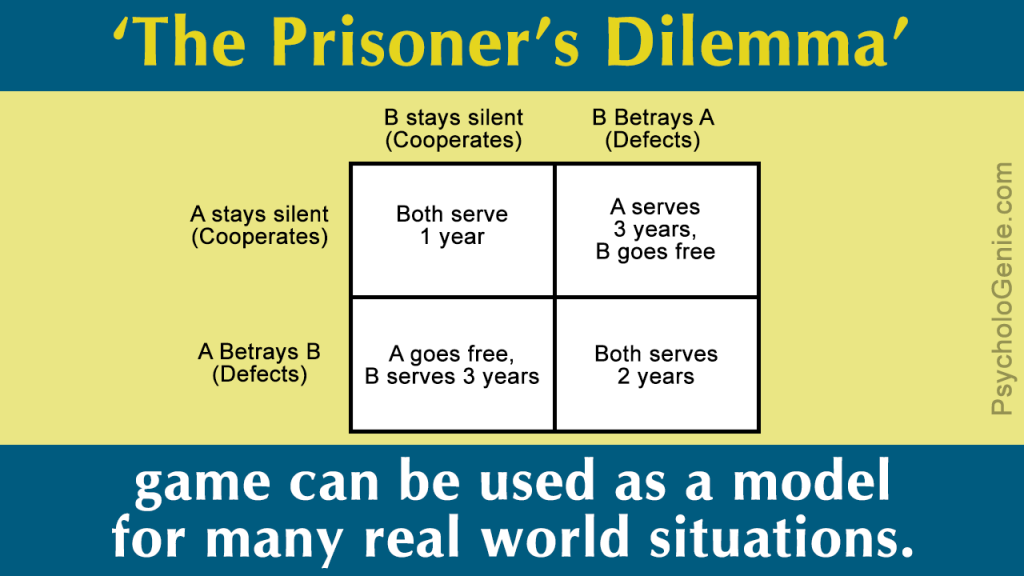
Every game has a set of prisoner’s dilemma rules that every player should follow. And iterated prisoner’s dilemma also has those kinds of rules. Knowing and understanding the rules makes playing the game easier and definitely more fun. So, following the rules is definitely important, although some of the rules can be changed depending on what you want. But, you should definitely never change the rules of the game too much, since it might not even be recognizable without all of its rules being changed.
Two people are supposed to be separated, whether they would be separated into two rooms or any other way. They are to choose between cooperate or defect, and if both parties choose to cooperate, they are then rewarded with a R.
So, that’s it about iterated prisoner’s dilemma and how to play it. Hopefully, this does help you know what you should do if you ever want to play this game. This game is definitely fun, especially as long as you play, it will all of the right people.… Read the rest